Para recordar

¿Qué sabemos de las funciones seno, coseno y tangente?

Las funciones SENO, COSENO Y TANGENTE  surgen a partir de la representación gráfica de las razones trigonométricas seno, coseno y tangente en una circunferencia trigonométrica, es decir, de radio de una unidad. A cada valor de un ángulo le corresponde un determinado valor, lo cual se representará en los ejes cartesianos. 

Visualiza los siguientes videos y luego realiza los gráficos de las tres funciones en tu carpeta: 

¿Cómo resolvemos un triángulo que no es rectángulo?

Si necesitamos conocer los lados y ángulos de una triángulo acutángulo u obtusángulo, no podemos aplicar las razones trigonométricas seno, coseno o tangente.

TRIÁNGULO ACUTÁNGULO

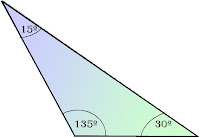                 TRIÁNGULO OBTUSÁNGULO

Por esta razón es necesario aplicar el Teorema del SENO ó el TEOREMA DEL COSENO dependiendo de los datos con que se cuente. 

Visitá el  siguiente sitio web y visualiza el siguiente video para comprender mejor los conceptos: 


LEY DE COSENOS


LEY DE SENOS

¿QUÉ SON LAS RAZONES TRIGONOMÉTRICAS?

Se llaman razones trigonométricas a aquellas que relacionan las longitudes de los lados de un triángulo con los ángulos del mismo. Las razones trigonométricas dependen del ángulo considerado.

En un triángulo rectángulo,  el lado opuesto al ángulo recto se llama hipotenusa y los otros dos lados  catetos. Para cada uno de los  ángulos agudos de un triángulo rectángulo, uno de los catetos es el adyacente y el otro es el opuesto.

Las razones trigonométricas se definen de la siguiente manera:

SENO de un ángulo: es la razón entre el cateto opuesto y la hipotenusa.

COSENO de un ángulo: es la razón entre el cateto adyacente y la hipotenusa.

TANGENTE de un ángulo: es la razón entre el cateto y el cateto adyacente.

A resolver

La puerta de entrada  del edificio donde viven Camila  y Pablo  se halla a varios metros sobre el nivel de la vereda y se accede a él por una rampa o subiendo una escalera. Si los chicos caminan 2 metros por la rampa, se encuentran a 1 metro del piso y si recorren 2 metros por la escalera (refiriéndonos al alcance de la escalera) están a 1,5 metros  del piso.

¿Qué sucede si caminan 1 metro por la rampa o  por la escalera? ¿A qué altura se encuentran del piso en cada uno de los casos?

Grafica la situación en cada uno de los cuatro casos y  calcula el cociente entre la altura y la distancia  recorrida, ¿Crees que existe alguna relación entre  los resultados obtenidos? Observa también la relación entre la amplitud de los ángulos formados entre la escalera y el piso y la rampa y el piso. 

RESUELVE LA ACTIVIDAD Y  PUBLICÁ TUS RESPUESTAS EN ESTE ESPACIO.

 ¡ADELANTE!

Primera Actividad

Investiga en grupo de no más de cuatro alumnos sobre los orígenes de la Trigonometría teniendo en cuenta el texto leído anteriormente.


Luego expongan sus investigaciones en este espacio

¡ A trabajar!

¿Historia?¿ O Matemática? Nooo.. ¡Historia de Matemática!

¿Qué es la TRIGONOMETRÍA?

La trigonometría es la rama de la matemática  que estudia las relaciones entre los lados y los ángulos de un triángulo.

El estudio de la trigonometría es muy interesante ya que permite resolver una gran cantidad de situaciones y problemas en el mundo real, resultando fundamental especialmente en cualquier tipo de aplicación basada en medidas y distancias.

De hecho sus primeras aplicaciones fueron en el ámbito de la astronomía y la navegación; casos en los que no es posible hacer mediciones de manera directa o donde las distancias son inaccesibles, como la distancia de la Tierra a la Luna o la medida del radio del Sol.

¿Cuáles son los orígenes de la Trigonometría?

El documento más antiguo con procedimientos matemáticos, es el papiro de RHIND. En la construcción de pirámides egipcias un problema fundamental era mantener una pendiente (inclinación) uniforme en cada cara y la misma en las cuatro caras. Este concepto llevó a los egipcios a introducir un concepto equivalente a la  de cotangente de un ángulo.

En la civilización griega, en cambio, la trigonometría surge gracias a las necesidades astronómicas, ya que se requería la medición de ángulos y arcos cada vez con mayor exactitud. Erastótenes de Cirene, midió la distancia real de la Tierra al Sol y de la Tierra a la Luna, a partir del radio terrestre. Hiparco de Nicea, Menelao de Alejandría y finalmente Ptolomeo desarrollaron casi toda la Trigonometría que se conoce hasta la época.

En la India, se adquirieron los conocimientos de Ptolomeo, pero los transformaron a la forma en cómo se trabaja en la actualidad. Mientras que la trigonometría de Ptolomeo se basa en la relación funcional, los arcos ó ángulos centrales  en una circunferencia y las cuerdas que ellos subtienden, los matemáticos indios transformaron esta relación y la convirtieron en el estudio de la correspondencia entre la mitad de la cuerda y la mitad del arco o ángulo central subtendido por la cuerda total. Así fue como nació, el antepasado de la función trigonométrica que hoy en día se conoce como FUNCIÓN SENO.